Down the middle!

Various indicators can be used to analyse values. The most common are maximum, minimum and average. However, the median also often plays a role. In the following article, I would like to explain what the median is and how it can be calculated in conzept 16.

What is the median?

The median is the mean value of a sorted sequence. The median is always the value in the middle of this sequence. For example, in a sequence of seven values, the median corresponds to the fourth value.
With an odd number of values, the median is exactly in the middle, but these values must be sorted according to size.

If there is an even number of values, the median is calculated slightly different. The lower and upper median are sought first. These are the two values that lie in the middle and represent the upper and lower limits. The actual median can be determined from these. To do this, the average of the lower and upper median is calculated. With eight values, for example, the fourth and fifth values are added together and divided by two. The result is then the median.

Median vs. Average

In contrast to the median, all values are added together in the average value and divided by the number of values. This method has the disadvantage that the average value can be very strongly influenced by the individual values.
I would like to illustrate this with a small example.

We have the following values in a table:

• 75
• 80
• 83
• 90
• 96
• 105
• 135
• 165
• 200

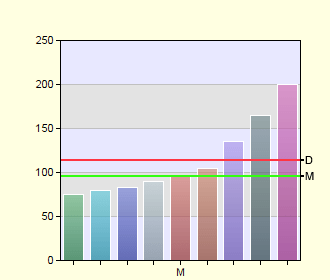Ratio of median and average

The average value from these values is 114.33. From this we could conclude that the value 114.33 is an ordinary value in the table. However, this would be wrong. The average has been greatly altered by the last 3 values.

The median in this example is 96, as this is exactly in the middle. According to it, we could assume that an ordinary field has approximately the value 96. The median divides the values in half so that there are an equal number of values greater and less than it. The median is insensitive to outliers.

Der Median in conzept 16

Wouldn’t it be interesting to determine the median of a certain field from a table? This is possible with the help of procedure Fnc.Aggegrate provided for download below. This allows you to easily determine the smallest, the largest, the average and the median. We have field ffSlsSolds of type float. This field contains the turnover on a specific date. We sort this field using a selection and then enter the corresponding content, depending on which aggregations were selected.

For the median, for example, this is how it looks:

// Median that is supposed to be determined
if (aAggregations & _Rec.AggMed != 0 and vCount > 0)
{
  // Determine median position
  tMedPos # ((vCount - 1) / 2) + 1;
  // Determine median
  if (
    // Read first data record
    RecRead(aTblNo, tKeyOrSel, _RecFirst) = _rOK and
    // Median position = 1
    tMedPos = 1 or
    // Read data set at median position
    RecRead(aTblNo, tKeyOrSel, _RecNext, 0, (tMedPos - 1)) = _rOK)
  {
    // Differentiation via data type
    switch (tFldType)
    {
     // Data type = float
     case _TypeFloat   :
      {
        vMed # FldFloat(aTblNo, aSbrNo, aFldNo);
        // If the number of data sets is even and the next data set could be read
        if (vCount % 2 = 0 and RecRead(aTblNo, tKeyOrSel, _RecNext) = _rOK)
          vMed # (vMed + FldFloat(aTblNo, aSbrNo, aFldNo)) / 2\f;
      }
      //...
    }
  }
}

The function Rec.Aggregate() has the following signature:

// +++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
// + Aggregate data sets                                   +
// +++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++

sub Rec.Aggregate
(
  aTblNo                : int;            // Table number
  aSbrNo                : int;            // Partial data set number
  aFldNo                : int;            // Field number
  aAggregations         : int;            // Aggregations
                                          //   _Rec.AggMin - smallest value
                                          //   _Rec.AggMax - largest value
                                          //   _Rec.AggAvg - average
                                          //   _Rec.AggSum - sum
                                          //   _Rec.AggMed - median
  aQuery                : alpha(4096);    // inquiry (optional)
  var vCount            : int;            // quantity
  var vSum              : float;          // sum
  var vMin              : float;          // smallest value
  var vMax              : float;          // largest value
  var vAvg              : float;          // average
  var vMed              : float;          // median
)
: int;                                    // result
                                          // = _ErrOk (0) : Success
                                          // < 0 : Error (See SelDefQuery, SelStore und SelRun)

Depending on which aggregations were specified, the corresponding values are returned to the variables declared with var. The number of aggregated values is always determined.

The function can aggregate fields of the following types:

• word
• int
• bigint
• decimal
• float

Example

The following function call determines the lowest, highest and median value of sales per day within the first quarter of 2013:

// Determine field
tField # 'ffSlsSold';

tResult # Rec.Aggregate(
  FldInfoByName(tField, _FileNumber),           // Table number
  FldInfoByName(tField, _SbrNumber),            // Partial data set number
  FldInfoByName(tField, _FldNumber),            // Field number
  _Rec.AggMin | _Rec.AggMax | _Rec.AggMed,      // Aggregations
  'fdSlsDate between [01.01.2013, 31.03.2013]', // Inquiry
  var tCount,                                   // Quantity
  var tSum,                                     // Sum
  var tMin,                                     // Smallest value
  var tMax,                                     // Largest value
  var tAvg,                                     // Average
  var tMed                                      // Median
);

In the function shown above, the aggregations _Rec.AggMin, _Rec.AggMax and _Rec.AggMed are passed. This means that the smallest value, the largest value and the median of field ffSlsSold are to be determined. A combination of all aggregations together is also possible. No aggregation is required to record the number of data records. The number of data records is always returned.
In the download you will find a database including data sets. Function Rec.Aggregate is included there and can be customised as required.